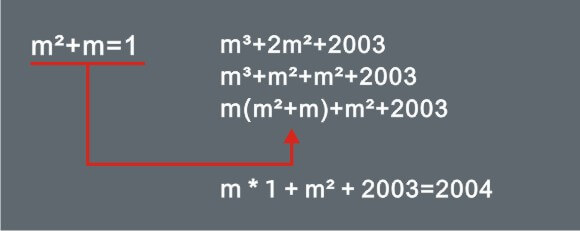通过条件可知，m平方+m的值等于1，后一代数式中将2m平方拆分后，可以提取公因数得到m（m平方+m），因为m平方+m的值等于1，所以m（m平方+m）的值就等于m；
求得的m与剩下的被拆分的m平方相加，又得到一个1，于是所求代数式的值应为2004。
发现目前博课写代数数很不方便，图解的方式未免过于消耗时间了，新的课题开启，支持代数式的显示。
通过条件可知，$ m^2+m $ 的值等于1，后一代数式中将$ 2m^2 $拆分后，可以提取公因数得到$m(m^2+m)$，因为$ m^2+m $的值等于1，所以$m(m^2+m)$的值就等于$m$。
移动端可扫我直达哦~
本文作者：Alphonse
本文链接：已知m平方+m-1等于0，求m立方+2m平方+2003的值 - https://www.abddb.com/mathematical_olympiad_algebra_replace.html
版权声明：如博文中无特别声明，即为站长原创文章，仅代表个人观点，版权归 小鸟数据 所有，如需转载，烦请注明出处！
初中的一道几何题，题目有误，原题要求AD的最小值，但最小值就不是类似下方的四边形了，而是类似蝴蝶翅膀的有交叉的图形。第二天孩子同老师确认后，老师也认为应该是求AD的最大值。其实说求最大值也不准确，将三角形ABN与CDN分别镜像后，可以...
一个学期结束，开学之初的知识基本已经还给了老师，一做练习，一问三不知，继续练吧，少年！排版两页，一页仅问题，一页含答案，双击任意单元格后按enter，会重新刷新题目。小学时间间隔运算
在孩子的试卷上与抛物线这个知识点久别重逢，颇有点“儿童相见不相识，笑问客从何处来”的寂寥。因为是超纲的卷子，所以临时用scratch展示了一下抛物线曲线的生成，但效果不是特别理想。第二天（也就是现在）在网上尝试搜索了一下在线绘制的工具...
偶然在抖音刷到这道题，因为主业是机械制图，所以画完图用工具直接测量了一下面积，在答案是40已经提前预知的情况，还是思考了好一会。一半模型，在这里应该是指长方形连接对角形成的三角形，其面积为长方形面积的一半，做了两条辅助线之后，答案就呼...
以数字2的幂运算为例，个人觉得，2的一次方，可以看成1x2，2的2次方，可以看成1x2x2，幂每次增加1，值就需要多乘以一个2，而幂每次减少1，就会少乘一个2，而从2次方到1次方的值，是从1x2x2变成了1x2，也可以理解成除以2。到...
与元角分的单一10进制不同，时间的的进制更为复杂一些，60秒为一分钟，60分钟为一小时，24小时为一天。因为它同时包含了两种进制,所以很多初学的孩子可能在时间的计算上会摸不着头脑,简单制做了一份excel练习表格,点击任意单元格并按回...
接触过几个小学阶段的孩子，同样的一类题型，有些孩子一听就会，有些则百思不得其解，虽然最终都能掌握，但所耗费的时间精力确实不可同日而语。虽然重复的讲解让人烦躁，但仔细想想，成人世界的唯金钱论也好，儿童时代的唯分数论也好，都是把所有人往一...
化简(1) $2(3x+2y)+2[x+2y-(x-y)]$参考答案：$6x+10y$(2) $(-a^2+2ab-b^2)-2(ab-3a^2)+3(b^2-ab)$参考答案：$5a^2-3ab+2b^2$计算(1) $-3x^2-...
化简(1) $2(3x+2y)+2[x+2y-(x-y)]$(2) $(-a^2+2ab-b^2)-2(ab-3a^2)+3(b^2-ab)$计算(1) $-3x^2-2x+5x^2+1+x$(2) $b+2(2a^2-b)-3(3a...
例题有一批货物需要从A地运往B地，货主准备租用甲、乙两·种货车，已知过去两次租用这两种货车运货情况如下表.现租用3辆甲种货车和5辆乙种货车，一次刚好运完这批货物，如果按每吨付50元计算，问货主应付运费多少元？ 次数 ...
类型一：一元一次方程的概念及综合应用1．已知 $3a^{m-1}b^2$ 与 $4a^2b^{n－1}$ 是同类项，试判断 $x＝\frac{m+n}{2}$ 是不是方程 $2x－6=0$ 的解．2．已知 $(m－3)x^{|m|－2...
下表显示了某次钓鱼比赛的结果，上行的值表示钓到的鱼数，下行的值表示钓到n条鱼的参赛人数. 鱼获n 0 1 2 3 … 13 14 15 ...
