组合数逆推公式-利用c++求组合数

公式定义

组合数逆推公式是一种用于计算组合数的有效方法。它可以用来计算从n个不问元素中取出 m 个元素的组合数。它的公式为：C（n，m）=C（n—1，m）+C（n—1，m—1），其中 C（n，m）表示从 n个不同元素中取出m个元素的组合数， C（n—1.m）表示从n—1个不同元素中取出m个元素的组合数， C（n—1，m—1）表示从n—1个不同元素中取出m—1个元素的组合数。由此可见，组合数道推公式可以有效地计算组合数。

图解公式

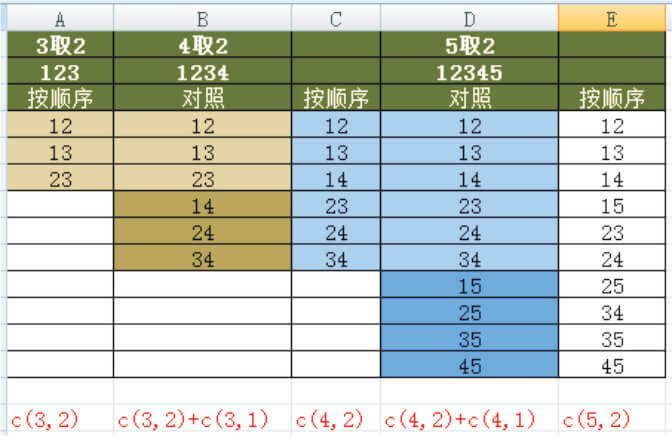
对比c（3，2）与c（4，2），其实部分结果是相同的，只是多了14、24、34这3个结果，而3这个值，可以理解为c（3，1），即从3个数中取出一次数，可以取几次。

应用公式后，我们可以将c（5，2）拆分如下，一直拆到c（2，2）只能有一种取法，遂人艰不拆。而所有的c（n，1）其返回值都是n，此时递归的公式已经呼之欲出了。

完整的程序

#include<iostream>

using namespace std;

int group(int n,int m){
    if(n==m){
    return 1;
    }
    if(m==1){
    return n;
    }
    return group(n-1,m)+group(n-1,m-1);
}

int main(){
    cout<<group(6,2)<<endl;    
}