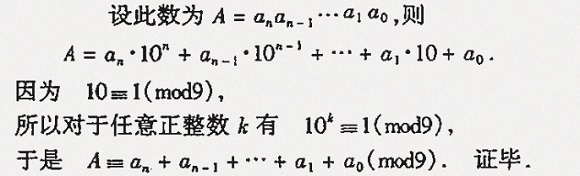求123456789......2012的除以9的余数

看到这么一道题目，问一个由连续自然数1，2，3，4，5。。。2012连接而成的超大数字，除以9后的余数是多少。因为计算器算力有限，想走个捷径提前看个答案逆向推导也推导不了，在纸上画了一下，发现从1开始的每9个自然数之和必然是9的倍数。

题目是把上述自然数连接成了一个巨大自然数的数位，而我们知道，数位之和为9的倍数的自然数是可以被9整除的，也就是说，123456789，123456...18，123456...27，这样的数字都可以被9整除，每向后增加9个自然数，都会出现一次这种情况，所以利用2012除以9，得数为223余5，也就是说，可以被9整除的数段之外，还多出了5个自然数。

接下来就只需要关心这余下的几个数就可以了，连起来看的话，得到这样一个数字：20082009201020112012。我们需要利用这样一个定理：一个自然数除以9的余数等于这自然数每个位上数字之和除以9的余数。顺手附上这个定理的求证过程：

20082009201020112012各数位之和为60，所以可以得出结论，这个巨大的自然数，除以9之后余数为6。