在之前的教程中,我们曾经实现过一个跑酷游戏,通过固定人物,不断平移背景来实现移动效果。在滚动长方体这个小游戏中,博主把长方体的活动范围也限定在了原点附近,所以同样需要移动地图来衬托长方体的移动。
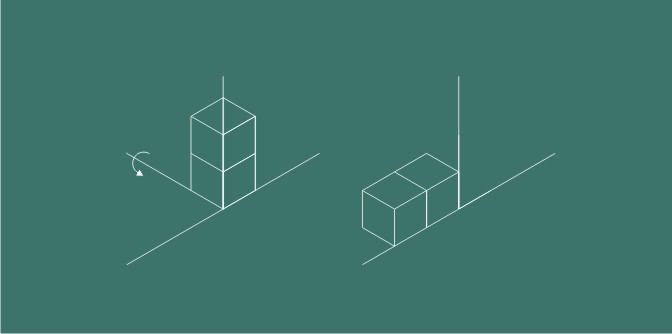
一个长方体,绕某根坐标轴旋转的时候,不出意外应该是类似上图的情况。
因为博主在移动过程中不断的平移长方体的坐标,所以最终的效果是坐标轴类似一堵墙,长方体倚着这堵看不见的墙慢慢滑下,最终仍旧紧贴着坐标轴。
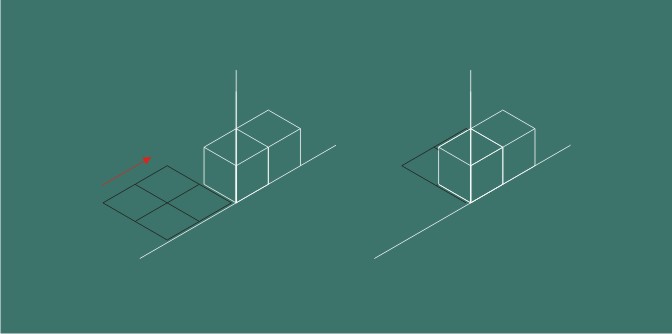
通过观察原点附近的长方体角点,可以发现,在旋转90度后,这个角点被向右移动了2个方格的距离,我们通过将地图背景同步向右移动两个方格的距离,来辅助展现这个移动的过程。
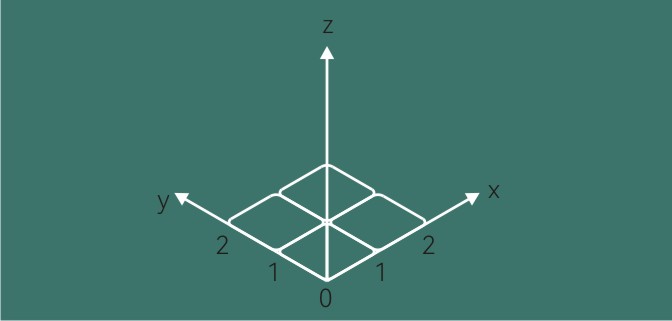
平面坐标转换为2.5D等距视图下的坐标
按照网上普遍的说法,等距视角(2.5D)视角,视觉上是把一个正方形旋转42度,然后垂直方向压缩到一半的高度,这样压缩后得到的菱形的尖角大约是53度左右,因为60度的等边三角形比较容易画,所以博主直接画了一个尖角为60的菱形。对比过几张等距视角的图片,发现这个角度因个人喜好而异,并没有固定的标准。
以60度的菱形为基准的等距坐标转换的经验公式如下:
等距x坐标
-> sin60度*(平面x坐标-平面y坐标)
等距y坐标
-> sin30度*(平面x坐标+平面y坐标)
等距z坐标
-> sin30度*(平面x坐标+平面y坐标)+ 平面z坐标(这么说可能不太准确)这个公式只是根据自己的需求总结,未经严格测试,供大家参考,在博主利用画笔绘制等距立方体时测试有效。
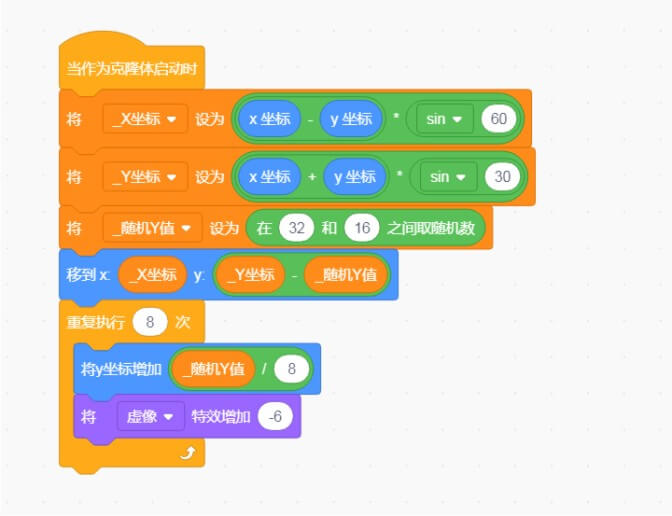
生成地图的逻辑如下,先通过平面布局,将克隆体安排就位;
为克隆体设置两个私有变量“_x坐标”,“_y坐标”,利用前文所列公式,将转换后的坐标存入这两个变量,最后移动到“_x坐标”,“_y坐标”。
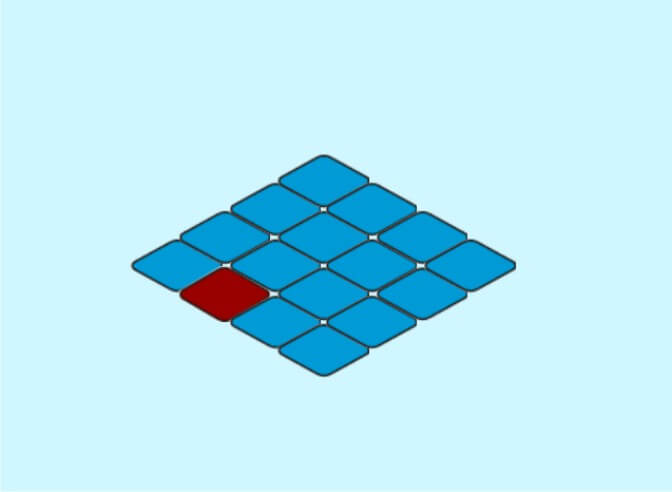
实际生成的地图如下,地图转换后可能出现平面显示时正常的图块,转换后坐标超出屏幕极限被挤回的情况,博主考虑的解决方案是去比对一下私有的“_x坐标”,“_y坐标”是否超出屏幕,如果超出屏幕则暂时隐藏。因为后续我们移动时会增大或减小这两个值,当坐标值满足条件时(未超出屏幕不会被挤压的情况),再重新显示克隆体。
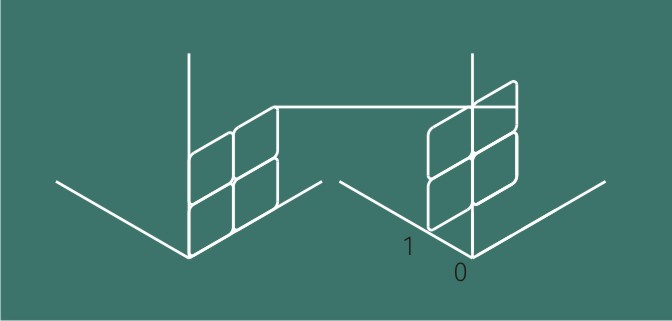
在《Scratch中等距视角下长方体的滚动动作》一文中我们实现了立方体的原地滚动,我们可以伴随立方体的动作,同时向地图角色发送消息,通知由克隆体组成的地图背景进行相应的移动。