N皇后问题
在一N*N(N<=10)的棋盘上放N个皇后,使得它们不能相互攻击。两个皇后能相互攻击当且仅当它们在同一行,或者同一列,或者同一条对角线上。找出一共有多少种放置方法。
程序全文
#include<iostream>
using namespace std;
int sum=0,a[9],n;
bool d[16]={0},b[9]={0},c[16]={0};
int search(int);
int main(){
cin>>n;
search(1);
cout<<sum<<endl;
return 0;
}
int search(int i){
if(i==n+1){
sum++;
//for(int k=0;k<9;k++){
// if(a[k]!=0){
// cout<<a[k]<<","<<k<<endl;
// }
//}
//cout << endl;
return 0;
}
for(int j=1;j<=n;j++){
if(!b[j]&&(!c[i+j])&&(!d[i-j+n])){
//a[i]=j;
b[j]=1;
c[i+j]=1;
d[i-j+n]=1;
search(i+1);
b[j]=0;
c[i+j]=0;
d[i-j+n]=0;
}
}
}注释部分是自己添加的输出具体点位的输出语句,参考逻辑时可以忽略;同样if部分语句也只是在循环满足条件后sum++统计结果,也可以忽略不看,关键的逻辑在for循环内。而for循环内主要就是递归前的3个标记值:
b[j]=1;
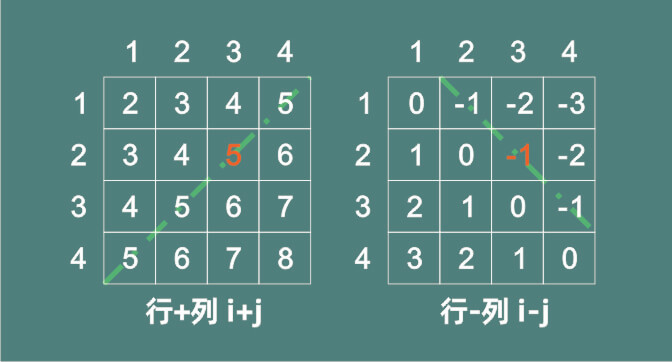
c[i+j]=1;
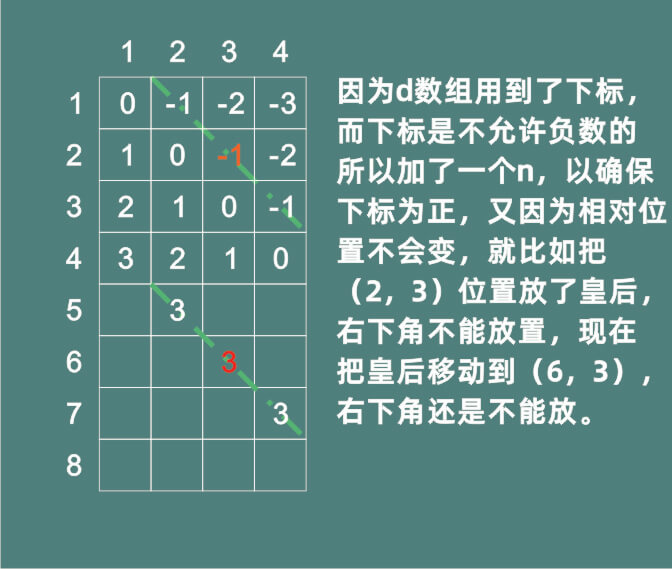
d[i-j+n]=1;关于b[j]
当i(行)、j(列)均为1时,程序走第一个循环,b[j]被设置为1,在下一个search(i+1)里,因为j始终从1开始,所以第二行第一格时,因为b[j(j=1)]已经有值,所以if语句块被跳过,也就实现了列方向上的过滤;