c++八数码问题与宽度优先搜索

八数码问题

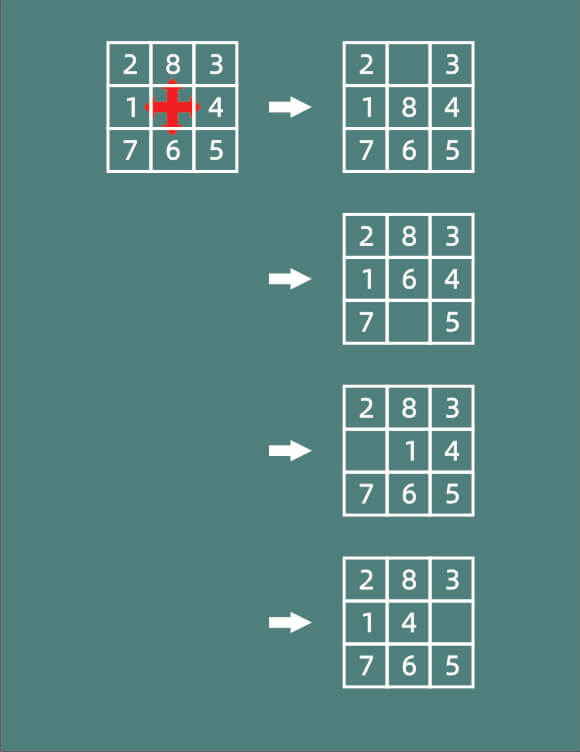
在3行3列的9宫格中，有8个格子放有1～8之间不同的数字，余下一个空格，这个空格可以在格子内上下左右地移动位置。现在给你初状态和目标状态，请你找出最少的移动步数。

如图所示，左边是初始状态，右侧为目标状态，这同样是noi官方培训视频中的一道题目。

解题思路

有点类似拼图游戏的逻辑，我们首先定位空格，因为允许上下左右移动，所以至多会出现4种新的结果，因为有边界的存在，4种结果有时会缩减至两种，又因为我们不希望又前进一格后又退回的骚操作，所以经过筛选，符合条件的结果可能会更少。

数组的选择

一维数组或二维数组都可以解决这个问题，二维判断边界更为简单粗暴，但是涉及到值的交换，数据提取时，又不如一维数组直观，一维数组在空格的移动上需要更复杂的判断，但实际程序编制过程中个人感觉还是一维数组更为直观。

程序逻辑

设置一个数组，用来存储每个阶段的数据，设置st，ed两个变量，分别代表数组的头部与尾部。比如第一步产生了4个状态，我们将这四个状态暂存，每加入一个新状态，尾部就后移一位。头部变量每增加一次，就检测一次4个方向上的可能性，继续将新状态存入。因为前期可允许的走法较多，st与ed的间隔会逐渐拉大，因为查重筛选的存在，后续新的状态会逐渐减少。

将数据存入前先检测一下是否当前已有的结果重复，重复就中止存入。存入后再核对一下目标数组，如果与目标数组一致，则目的已达到，中止所有程序。

一维数组的方式

#include<iostream>
using namespace std;

int bfs(){
    //目标数组
    int target[9]={1,2,3,8,0,4,7,6,5};
    //存储结果，多一位存储步数，初始步数0 
    //注意二维数组的定义方式 
    //思考更多维数组的定义 
    int result[255][10]={{2,8,3,1,0,4,7,6,5,0}};
    //定义临时存储数组
    int next[10];
    //定义方向数组上下左右，9宫格，减3即向上，减1即向左
    //行数列数不定时则需要考虑使用变量输入 
    int arrow[4]={-3,3,-1,1};
    //定义起始中止的数组下标
    int st=0,ed=1;
    //定义space代指空格位置；
    int space=0; 
    //定义计数器count
    int count=0; 
    

    //每增加一个正确结果则ed+1，所以两者间距会先加大，因为有去重，后逐渐缩小 
    while(st<ed){
        //因为每个空格都可能有4个方向，先循环4次遍历arrow
        for(int i=0;i<4;i++){
            //提取结果中的第一组存入next
            //提取结果符合条件的需要进行数据交换 
            //需要保留原始数据
            //所以存入临时数组
            for(int j=0;j<10;j++){
                next[j]=result[st][j];
                //取值同时顺便找一找空格在哪 
                if(next[j]==0&&j!=9){
                    space=j;
                }
            }
            //注意这里的循环数i，与j不同，因为后续还需要用到，所以不能重新定义
            //space是指空格的位置，arrow[i]是指移动方向数组的对应值，比如空格在5，i是0
            //arrow[i]=-3，即向上移动一格，因为i会循环四次，即遍历4个方向
            //现在判断边界；
            //首先一维数组不能超限； 
            if( (arrow[i]+space)>=0 && (arrow[i]+space)<=8 ){
                //如果靠左，下标为0，3，6时禁用-1，因为过界了。  
                if( (arrow[i])%3==0 &&  arrow[i]==-1 )continue;
                //如果靠右，下标为2，5，8时禁用+1，因为过界了。 
                if( (arrow[i])%3==2 &&  arrow[i]==1 )continue;
                //判断结束执行移动
                next[space] = next[arrow[i]+space];
                next[arrow[i]+space] = 0;
                //步骤数加1 
                next[9]++;
                //去重操作，从resut第一组数据开始，到ed为止，设置一个计数变量count，
                //有一个相等就count+1，如果最终count数值为9，说明有完全重复的数组，
                //那么新数据就抛弃不用
                for(int k=0;k<ed;k++){
                    for(int l=0;l<9;l++){
                        if(next[l]==result[k][l])count++;
                    }
                    if(count==9){
                        break;
                    }else{
                        count=0;
                    }
                }
                //判断count最终值,不等于9则存进result数组
                //因为ed指向的是数组的尾部，所以直接存入ed指向的数组，存储结束ed+1 
                if(count!=9){
                    for(int m=0;m<10;m++){
                        result[ed][m]=next[m];
                    }
                    ed++;
                    //判断结果是否与target相同
                    //首先count清零
                    //结果对上就　break掉 
                    count=0;
                    for(int n=0;n<9;n++){
                        if(next[n]==target[n])count++;
                    } 
                    if(count==9){
                        cout << "get it!" << endl;
                        for(int m=0;m<10;m++){
                            cout << next[m] <<" ";
                            if((m+1)%3==0)cout << endl;
                        }
                        cout << endl;
                        break;
                    }else{
                        count=0;
                    }
                }
            } 
        } 
    st++;    
    } 
}

int main(){
    bfs();
}

二维数组的方式

尝试了一下二维数组的方式，感觉提取数据与数据交换时较为繁杂：

#include<iostream>

using namespace std;

int bfs(){
    //起始与中止下标 
    int st=0,ed=1;
    //查找空值
    int space[2]={0,0}; 
    //统计重复
    int count=0; 
    //储存结果数组
    int ranks[200][4][3]={{{2,8,3},{1,0,4},{7,6,5},{0,}}};
    //暂存数组 
    int next[4][3];
    //目标数组
    int tar[3][3]={{1,2,3},{8,0,4},{7,6,5}};
    //方向数组
    int arrow[4][2]={{-1,0},{0,1},{1,0},{0,-1}};
    while(st<ed){
        for(int i=0;i<4;i++){
            //循环取数 
            for(int j=0;j<4;j++){
                for(int k=0;k<3;k++){
                    next[j][k]=ranks[st][j][k];
                    if(j<3&&next[j][k]==0){
                        space[0]=j;
                        space[1]=k;
                    }
                }
            }
            //添加方向
            if(arrow[i][0]+space[0]>=0&&arrow[i][0]+space[0]<=3&&arrow[i][1]+space[1]>=0&&arrow[i][1]+space[1]<=3){
                next[space[0]][space[1]]=next[arrow[i][0]+space[0]][arrow[i][1]+space[1]];
                next[arrow[i][0]+space[0]][arrow[i][1]+space[1]]=0;
            } 
            //检验数据
            for(int l=0;l<ed;l++){
                for(int m=0;m<3;m++){
                    for(int n=0;n<3;n++){
                        if(next[m][n]==ranks[l][m][n])count++;
                    }
                }
                if(count==9){
                    break;
                }else{
                    count=0;
                }
            }
            //检验count并入队 
            if(count!=9){
                for(int m=0;m<3;m++){
                    for(int n=0;n<3;n++){
                        ranks[ed][m][n]=next[m][n];
                    }
                }
                ranks[ed][3][0]=next[3][0]+1;
                ed++;
            }
            //检测结果
            count=0;
            for(int m=0;m<3;m++){
                for(int n=0;n<3;n++){
                    if(next[m][n]==tar[m][n])count++;
                }
            }
            if(count==9){
                cout << "get it !!!" << endl << endl;
                for(int m=0;m<3;m++){
                    for(int n=0;n<3;n++){
                        cout << ranks[ed-1][m][n] << "  ";
                    }
                    cout << endl ;
                }
                cout << endl << ranks[ed-1][3][0];
                return 0;
            }
             
        }
        st++;
    }
}
int main(){
    bfs();
}